2021. 4. 29. 19:56ㆍ개발공부/자료구조 알고리즘
- Trees data structure is much faster than liner data structures, such as arrays or linked lists.
- non liner data structure is much more richer than simple "before" and "after" data structure.
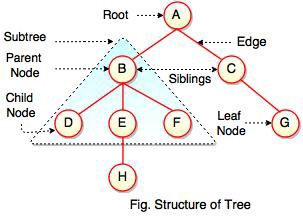
- The relationships in trees are hierarchical.
- Formal Tree Definition(Look for keywords)
. internal/external : with or without child nodes.
. edge : a pair of parent, child node.
. path : sequence of nodes.
💡accessor method : simply getting method, query method : find information and declare.
- Define Tree interface
. Generics : generics help you detect bugs during compile time and this is helpful since run time bug can be more problematic.
. <E> : when actual method is invoked, argument is substituted for formal type parameter.
Java Generics Tutorial, Generics Introduction
|
1
2
3
4
5
6
7
8
9
10
|
//Before implementing Generic
List myIntList = new LinkedList(); // 1
myIntList.add(new Integer(0)); // 2
Integer x = (Integer) myIntList.iterator().next(); // 3
//After implementing Generic
List<Integer>
myIntList = new LinkedList<Integer>(); // 1'
myIntList.add(new Integer(0)); // 2'
Integer x = myIntList.iterator().next(); // 3'
|
cs |
💡Difference btw interface and abstract class is method definition existence.
. So if abstract classes implements an interface, there is less work remains to complete a concrete implementation.
- Binary Trees
. An ordered tree every node has a most two children.
. A left child precedes a right child in order of children of a node
. Level of nodes = depth of nodes
. External node = Internal node + 1
- Implementation of LinkedBinaryTrees
. remove method defunct node conventionally delete every fields except parent, which refers node it self. It can be detected in validate().
. big(O) efficiency

- Array-Based Representation of a Binary Tree
. based on numbering position. numbering function is known as level numbering.
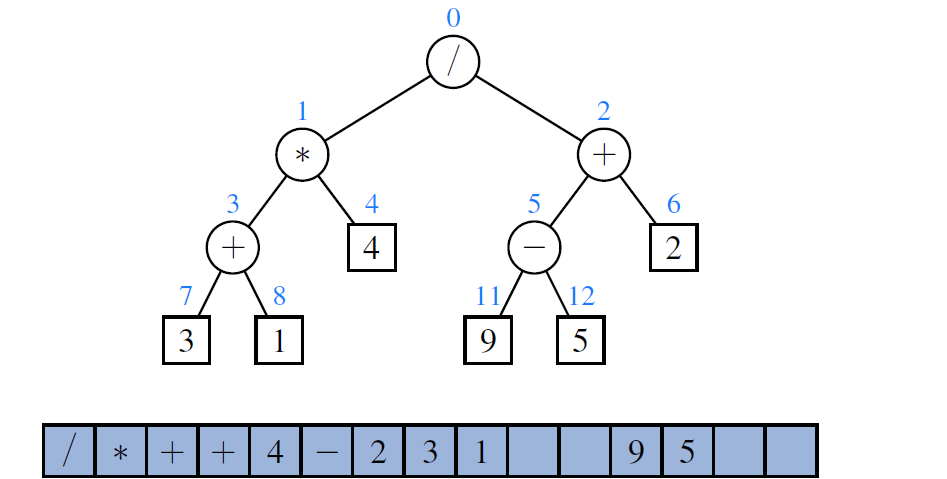
. numbering don't need to be consecutive. Numbering makes convert to Array easier.
- It depends deeply on shape of the Tree.
- Inefficient worst-case space usage can occur N(length) = 2n(square) - 1.
. But there are applications array representational binary tree space efficient.
. Another drawback is remove method. Not one child node moves location, all descendants of child.
- LinkedStructure in General(Not Binary) Tree
. Use collection(array or list) to work as a container in method children().
- Tree Traversal Algorithms
. Execute actions concerns with position p, traversal application might help increment performing complex computation for p.
. Preorder : perform visit root of T first then traverse child nodes recursively.
. Postorder : perform visit root of T last traverse child nodes first.
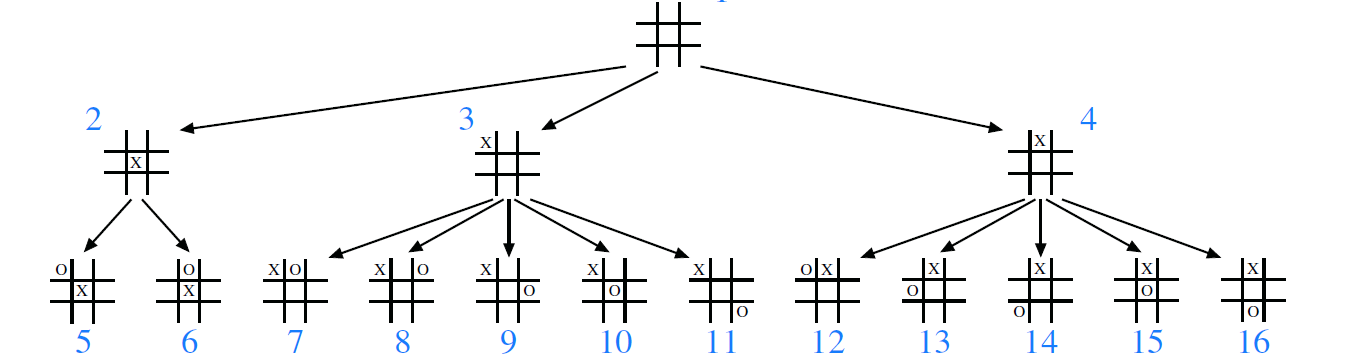
. Breadth-First Tree : visit all the positions at depth p first then move to depth p+1.
> Use widely in software for playing games → game tree seek possible choices player can make. root is initial configuration of the game(Tic-tac-toe)
> Main reason is that computer might not able to visit complete game, so visit breadth-first and response to certain moves.
> Pseudocode using queue(enqueue : insert from the end / dequeue : get from the front)
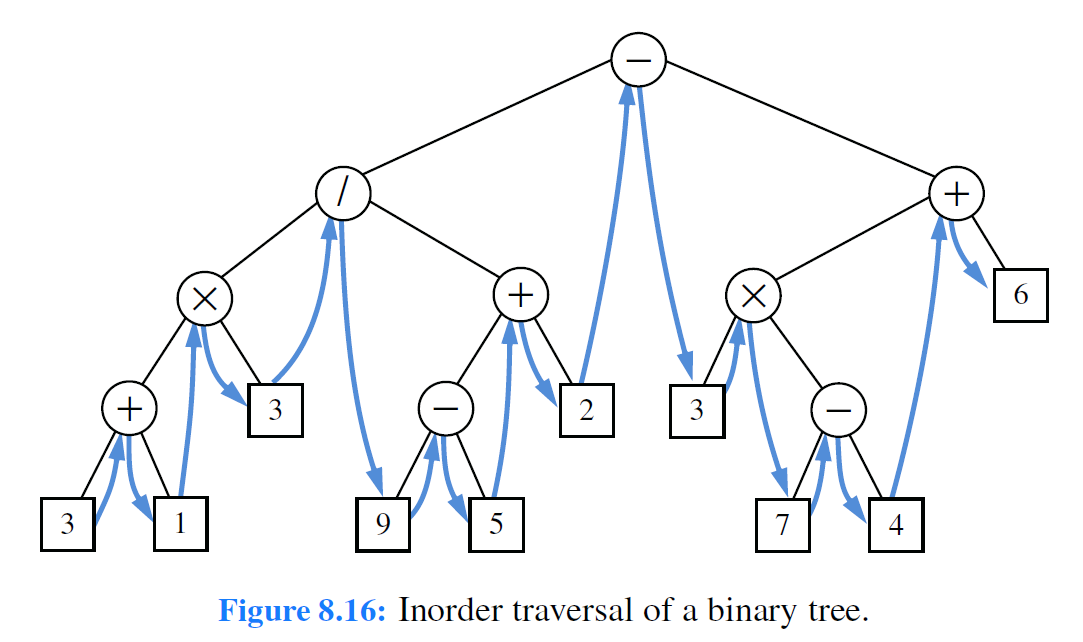
- Inorder Traversal of a Binary Tree
. visit position p after traverse left subtree then traverse right.
- Binary Search Tree
. ordered sequence of tree, binary search tree is used.
. It has order as below principles.

. Search for value v with position p element e(p). If v < e(p) visit to left, if opposite, visit to right, else equals found successfully.
. Big(O) takes from log(n+1) to n - 1 so binary search trees are most efficient when they have small height.
- Applications of Tree Traversals
. Table of Contents
> Insert indent(들여쓰기) using preorder(), invoking depth() to every position ends up with Big(O) asymptotically optimal(worsen as input increases). O(n2)
- Computing disk space
. Recursively visit all disk files then explicitly define whole disk space. So use postorder()
- Parenthetic Representations of a Tree
. Put trees into Computer friendly words, add parenthesis'()' and comma ',' with defining recursively.
- Using Inorder Traversal for Drawing
. left subtree → position p → right substree
- Euler Tours
. Type of traversal defined as "walk" from root toward leftmost child.
. Complexity of walk is O(n). There are two visits, pre visit(left toward down) and post visit(right toward up).
출처 : Data Structures and Algorithms in Java, 6th Edition 6th Edition (Michael T. Goodrich, Wiley)
'개발공부 > 자료구조 알고리즘' 카테고리의 다른 글
| [프로그래머스 스쿨] 알고리즘 - 1 (0) | 2023.06.28 |
|---|---|
| [Data Structure & Algorithm in Java 6th] Ch.3 Fundamental Data Structure (0) | 2021.05.19 |
| [Data Structure & Algorithms in Java 6th] Ch.10 - Hash tables (0) | 2021.05.12 |
| [Data Structures & Algorithms in Java 6th] Ch.10- Maps (0) | 2021.05.03 |
| [Data Structures & Algorithms in Java 6th] Ch.1 - Java Prmier (0) | 2021.04.29 |